In this appendix we outline a simple set theory description which illustrates the progressive approach to the evaluation of a candidate for the role of the Gawain-Poet, and apply some simple probability theory to an estimate of the population which contained the Gawain-Poet.
Any serious candidate proposed for the role of the Gawain-Poet must conform to many of the items contained in the template. One approach to illustrating the progress of conformance to the requirements is simple set theory using Venn diagrams. Let us, for example, consider five requirements. Providing these requirements are statistically independent, the ordering of the points has no significance. Consider the case where the Gawain-Poet must conform to the following five points:
-
Could be described as having a good general education.
-
Was familiar with the pentangle and its Christian and knightly symbolism.
-
Was very familiar with a nobleman's court, where he had considerable experience of courtly life, courtesy, feasts and religious observance.
-
Was intimately aware of the organisation and rituals of the hunt and the breaking of the kill.
-
Was closely associated with the death of a young girl, probably his or his patron's daughter.
The selection of points for this example corresponds to points 3.3-3.7 in the template (Section 3 above.)
We start with a large candidate population from the north west of England, and reduce that population by requiring the fulfilment of successive conditions: to be a member of the population, a candidate must not only have good education, but must also be familiar with the pentangle and its Christian and knightly symbolism, etc. Each successive condition is a further constraint upon the size of the set of possible candidates, which shrinks at the application of each constraint.
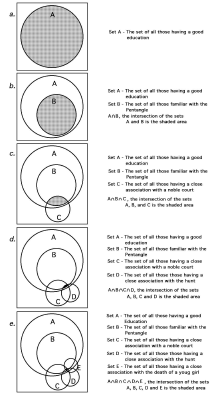
We assume that the Gawain-Poet was an Englishman[24] from the north-west of the country,[25] and aged between 20 and 50 at some time during the last decades of the fourteenth century. This sub-set of all Englishmen is then taken as the Universe of Discourse, represented by the rectangles[26] drawn around the circular sets in Figure A.1 where, schematically at least, the areas of the circles represent the sizes of the various sub-sets of the population; but see below for a more quantitative approach.
In figure a., the circle, A, represents the set of north-western Englishmen between the ages of 20 and 50 in the last decades of the fourteenth century who could be described as “educated”, men such as priests, lawyers, clerks, sons of local gentry and literary men etc. This set necessarily lies entirely within the Universe of Discourse, and the Gawain-Poet is required to be a member of this set.
In figure b., the circle B represents the set of those who were familiar with the pentangle and its Christian and knightly symbolism, (which is not necessarily a sub-set of A as in the figure.) Providing there is intersection between A and B, i.e. A∩B≠∅, where ∅ is the empty or null set, then the Gawain-Poet is to be found in the intersection, A∩B, which is shaded in the figure.
In figure c., the circle C represents the set of those who were very familiar with the ways of court. This set is not necessarily a sub-set of A or B, but must lie within the Universe of Discourse. Intersection with both A and B is required so that A∩B∩C≠∅. The Gawain-Poet is to be found in the smaller set A∩B∩C. If C does not intersect with both A and B, there is no north western Englishman who can satisfy all of the first three requirements.
In figure d., the circle D represents the set of those who had close knowledge of the procedures and rituals of the hunt. The same constraints on intersection are required, if the Gawain-Poet is be a member of the set A∩B∩C∩D≠∅.
In figure e., the circle E represents the set of those who had been closely associated with the death of a young girl before the age of two, and perhaps associated in some way with pearl. The Gawain-Poet is now restricted to the set A∩B∩C∩D∩E≠∅.
We can then, of course, impose further restrictions on the set containing the Gawain-Poet, and the number of members of the set continues to decrease.
If the sets are statistically independent, we have no reason to suspect the remote possibilities that that any two sets are equal, or that we have any supersets, so that the intersection set is necessarily becoming smaller with the application of each constraint. At the moment, however, we have no idea just how small it is getting, but if we could reduce the size of the final intersection set to one member, then we could say with some confidence that we have included sufficient requirements to allow us to identify the Gawain-Poet. Unfortunately a complete and unambiguous identification is only possible if we could populate the sets with real names. In the absence of real names we can still achieve something by estimating the sizes of the sets.
For a start we define the Universe of Discourse. We make a less restrictive estimate of the period the poems were written, and expand the period from 1380-1400 (see Section 3.1) to 1355-1405. This surely covers all reasonable estimates of the date of composition of the poems of the Nero A.x. The population which included the Gawain-Poet is the set of all men and women from the north west who are aged between 20 and 50 at some point in the period between 1355 and 1405. There are some obvious limitations to this population:
-
The range of birth dates covered is 1305-1385
-
The range of reaching maturity at age 20 is 1325-1405
-
The range of death dates at age 80 is 1385-1465
This selection, covering a possible span of 160 years, covers all previous estimates of the social and geographical group to which the Gawain-Poet belonged, not only adequately but with considerable leeway.
We have an estimate of the total population of Cheshire in 1377 provided by Russell [RUSSELL48], quoted by Bennett [BENNETT79], of 25,000. This is regarded by Bennett as probably somewhat low, but is perhaps not too far out, so we use this as the size of the 1377 part of an initial population set which contains the Gawain-Poet.
The population of individuals between the ages of 20 and 50 in the time range 1355 to 1405 is considerably larger than Russell's population estimate. Let us start by assuming that the population of Cheshire in this period increased from perhaps 21,000 in 1355 to 36,000 in 1405. This range includes Russell's estimate of 25,000 for 1377. (With the Black Death of 1369 active within this period, this is surely an over-estimate of population growth.) Next let us assume that one half of the population are between the ages of 20 and 50 at any given time, giving us initial and final populations of 10,500 and 18,000. Next assume that all 20-year-olds live long enough to pass the age of 50. (Significant loss by death between 20 and 50 must certainly have occurred, but we ignore it.) We next assume that population growth is linear, and if we treat each individual as a unique unit of population in each year, this leads to a very considerable over-estimation of the population in which the Gawain-Poet is to be found: 51×(18,000+10,500)/2 = 726,750. Individuals born between 1335 and 1355 all occur a total of 31 times in successive years, those born between 1305 and 1334 appear from 1 to 30 times, and those born 1356-1385 occur 30 to 1 times. Taking these duplications into account we estimate a total population of 20-50 year-olds in 1355-1405 of 471,833.[27]
Thus we have a population (our Universe of Discourse) of about 471,833 which contains the Gawain-Poet. If we were to restrict the population to men only, then we would halve this figure, but we do not impose this restriction; we allow for the equal possibilities that the Gawain-Poet might have been a man or a woman.
We can now make some reasonable assumptions about the constraints we impose upon this set. In all cases we will err very significantly on the generous side. How many of this population can we describe as possessing a “good general education”: perhaps 1 in 50.[28] How many were aware of the pentangle and were familiar with its Christian and knightly symbolism: perhaps 1 in 40.[29] How many were closely familiar with the ways of court: perhaps 1 in 20.[30] How many had considerable experience of the hunt, particularly with the strict conventions of the handling of the kill: perhaps 1 in 10. How many had an association with the death of a young girl, possibly his daughter or that of his patron: perhaps 1 in 5. How many had access to a good library: perhaps 1 in 10. And so on.
The portrayal of sets in Venn diagrams is most often arbitrary - as in Figure A.1 - but it is possible to make the sizes of the sets reflect the probability of membership of the sets, or to reflect geographical relevance as in [SAMUELS84]. In our case the ratio of the areas of the set A (education) and the Universe of Discourse is the probability of a member of the Universe of Discourse being a member of the set A. If we start with a square of side 10.0cm to represent the 471,833 population, then the set A, assuming a probability of 1 in 50, is a circle of radius 0.798cm and similarly the set B (pentangle, 1 in 40) has a radius of 0.892cm. If memberships of sets A and B are statistically independent, then the area of the interseection set A∩B is equivalent to a circle of radius 0.126cm, and of A∩B∩C (court, 1 in 20), 0.00282cm. - effectively invisible in a 10cm. square.
Perhaps it is worthwhile at this point that we should re-iterate that the sets A, B, C … are all independent subsets of the Universe of Discourse. That is, the members of the set B are all those who were associated with the Christian and knightly symbolic use of the pentangle, completely independently of their membership of any other set. If any set happens to be disjoint from the general intersection, e.g. if A∩B∩C∩D=∅, then we would have to conclude that no member of the Universe of Discourse could have been the Gawain-Poet. In general we expect that the complement of A relative to B is non-zero, i.e A\B≠∅ and similarly B\A≠∅. It is perfectly reasonable that a person closely associated with the death of a young girl might not be educated or aware of procedures at court etc., or that a person with knowledge of verbal contract had never read Roman de la Rose, but that person could not have been the Gawain-Poet The smaller the intersection between sets, the more rapidly the population of the intersection set containing the Gawain-Poet shrinks. In the following discussion and the table below (Table A.1,) we are dealing with a group of totally independent sets with non-zero intersections, A⊄B⊄C⊄D⊄E…etc. and A∩B∩C∩D∩E…etc.…≠∅. In principle it would be possible to allow for some dependences between sets by introducing correlation coefficients, but that seems to be straying a little too far from the available data.
Now we pull these estimates together and see how they limit the size of the set of persons from the north west in that period among whom the Gawain-Poet is to be found. In the table below (Table A.1) we successively apply these constraints and follow the decreasing size of the final set. In the table there is the assumption that the criteria are statistically independent. For example, if the probability of an individual possessing an education is 0.02 (1 in 50), and the probability of an individual being aware of the pentangle and its symbolism i.e. 0.025 (1 in 40), and if these two properties are independent, then the probability of an individual possessing both properties (i.e. being a member of both sets) is the product of the individual probabilities or 0.02 × 0.025 = 0.0005 (1 in 2000)[31]. The table shows the decrease in the size of the final set.
The purpose of the template for the Gawain-Poet is to insist that any candidate for the role of the Gawain-Poet must lie within the intersection of these 10 sets of north-western Englishmen. Conversely of course we are insisting that it would be very difficult (but perhaps not impossible) to accept that anyone for whom we have positive evidence that he did not fulfil all the requirements[32] of the template could have produced all the poems in the Nero A.x manuscript. Lack of evidence does not invalidate a candidate, but it does result in lower confidence. Finally note again that as our Universe of Discourse requires such properties as being an English man or woman alive at the right time and speaking a native north western dialect, these requirements cannot be included as separate requirements - they are present in the estimation of the population of the Universe of Discourse.
Table A.1. The Effect of Constraints upon the Size of the Population Set Containing the Gawain-Poet[33]
| Independent Requirement | Fraction of Population Assumed | Population of set Including the Gawain-Poet | Intersection Set |
|---|---|---|---|
| Universe of Discourse | all | 471,833 | |
| Educated (A) | 1 in 50 | 943.667 | (A) |
| Pentangle (B) | 1 in 40 | 235.917 | (A∩B) |
| Court (C) | 1 in 20 | 11.796 | (A∩B∩C) |
| Hunt (D) | 1 in 10 | 1.180 | (A∩B∩C∩D) |
| Girl (E) | 1 in 5 | 0.2359 | (A∩B∩C∩D∩E) |
| Library (F) | 1 in 10 | 0.0236 | (A∩B∩C∩D∩E∩F) |
| Legal (G) | 1 in 10 | 0.0024 | (A∩B∩C∩D∩E∩F∩G) |
| Port & storm (H) | 1 in 10 | 0.0002 | (A∩B∩C∩D∩E∩F∩G∩H) |
By the application of 5 constraints we have reduced the likely population of the group containing the Gawain-Poet to less than 1 (in fact 0.2359 or about 4.24 to 1 that we have found the Gawain-Poet). If we find a candidate satisfying these 5 constraints, we can be moderately confident that we have identified the Gawain-Poet. If we find the candidate satisfies still more constraints, we increase our confidence that we have identified the right man. A population of individuals is necessarily quantised and one must query the meaning of fraction population figures in this table. We use the reciprocal of fractional populations as a measure of the odds against a candidate meeting all these requirements by chance,[34] and if we find a candidate meeting all 8 of the above constraints, yielding an overall population of 0.00023592, this would imply that the odds that this candidate was in fact the Gawain-Poet would be about 4,238 to 1 on. In the case of James Cottrell where we have no direct evidence of his education, and can only infer it from his duties, if we omit the education requirement from our list of proven qualities, the population of the remaining 7 requirements is 0.0117958 and the odds that we have found the Gawain-Poet about 85 to 1 on that we have identified James Cottrell as the Gawain-Poet (170:1 if we were to exclude the possibility of the Gawain-Poet being female.). Arbitrarily we might say that any odds greater than 50 to 1 represent a near certainty. In addition to this application of the template to James Cottrell, we find (Section 4) another 23 parallels between the life of James Cottrell and the work of the Gawain-Poet which must boost our confidence level still further.
To get some feeling for the sensitivity of this population analysis, we present in Table A.2 the odds against fortuitous multiple coincidences for probabilities (fractions)[35] of 0.02 (1 in 50), 0.05 (1 in 20) and 0.1 (1 in 10) when we set all 8, 7, 6 or 5 of the requirements in Table A.1 to the same value.
Table A.2. The Sensitivity of Constraints and Probability upon the Population Set Containing the Gawain-Poet
| Fraction of Population | All 8 Requirements | 7 Requirements | 6 Requirements | 5 Requirements | ||||
|---|---|---|---|---|---|---|---|---|
| Population | Odds | Population | Odds | Population | Odds | Population | Odds | |
| Total population=471,833. Equal probabilities for all requirements. 8 requirements: education, pentangle, court, hunt, girl, library, legal, port. 7 requirements: pentangle, court, hunt, girl, library, legal, port. 6 requirements: education, pentangle, court, hunt, library, legal. 5 requirements: pentangle, court, hunt, library, legal. | ||||||||
| 1 in 50 | 0.00000001843 | 82,788,825 | 0.0000006040 | 1,655,776 | 0.00003020 | 33,15 | 0.001510 | 662 |
| 1 in 20 | 0.00001843 | 54,256 | 0.0003686 | 2,713 | 0.007372 | 136 | 0.1474 | 7 |
| 1 in 10 | 0.0047183 | 212 | 0.047183 | 21 | 0.4718 | 2 | 4.7183 | 0.2 |
If we set all 8 probabilities to 1 in 10, the odds are about 212 to 1, or omitting the education requirement, about 21 to 1 against a fortuitous set of chance occurrences. The technique is very sensitive to the probability assigned, but any fractions less than 1 in 10 are adequate for considerable confidence. The number of criteria required is also very important but six constraints with probabilities of 1 in 10 is sufficient to produce odds of two to one against a fortuitous set of coincidences. Clearly the estimates of probabilities in Table A.1 are wildly optimistic, it is highly improbable that 1 in 40 of the population of people between 20 and 50 in the north west of England in the last decades of the fourteenth century were aware of the Christian and knightly symbolism of the pentangle.
Alternatively,accepting the probabilities assigned in Table A.1, and taking the stand of devil's advocate, we can be much stricter and rule out 2 of the criteria as possible imaginative exercises (girl and port/storm.) Taking the remaining six criteria (education, pentangle, court, hunt, library, legal) as necessary and independent requirements for the Gawain-Poet we arrive at 0.0117958 in a population of 471,833, or 85 to 1 that we have found the Gawain-Poet.We see that even if we eliminate education as well, the five remaining requirements (which reduce the population containing the Gawain-Poet to 0.59) are adequate to define a template.
This set theory approach is not new to the field, it is a formalisation of the technique used by McIntosh, Samuels and collaborators in many papers culminating in the Linguistical Atlas of Late Middle English [MCINTOSH86]. If we extract a portion of the final (e.) Venn diagram above Figure A.1, we get something similar to the figures in e.g. Samuel's analysis of the geographical location of origin of the Harley Lyrics manuscript [SAMUELS84]. Although in the geographical location analysis, use can be made of the concept of being “outside a geographical set”, this is not particularly useful in the identification of the Gawain-Poet; adding in restrictions such as “he did not write Piers Ploughman or Canterbury Tales” does not help very much - although they may well be true. The comparison between Figure A.1 figure e. and the illustrations in Samuel's paper are shown below in Figure A.2.
Figure A.2. A Region of the Venn Diagram in Figure A.1 Compared with Extracts from the Figures in [SAMUELS84]
![A Region of the Venn Diagram in Figure A.1 Compared with Extracts from the Figures in [SAMUELS84].](images/setse123SS.gif) |
[D]
From left to right the diagrams are extracts from Figure A.1 and Figures 1, 2, and 3, from [SAMUELS84].
In the first extract from Samuel's paper (figure b.) we see county boundary lines, which help us to visualise the space, but are not relevant to the argument. The numbered lines represent parts of set boundaries for specific dialectical features, which are also related to geographical location, and the letters are members of the sets defined by the numbers. The progressive narrowing down of the geographical area where the Harley Lyrics manuscript might have been produced, by the addition of more constraints (set boundaries for specific dialectical features) is shown in the figure.
[24] “Englishman” should be read as a generic term for “Englsh man or woman” everywhere in this work. the term “Englishperson” is just too affected and inelegant for use. It is quite possible that the Gawain-Poet was a woman. However, the close description of what were primarily male and knightly procedures such as the arming sequence and the breaking of the kill make it less likely that the Gawain-Poet was female. There were indeed important female writers of this period, but it would be difficult to imagine that Julian of Norwich was familiar with the arming sequence and the breaking of the kill. Nevertheless we make no assumption about the sex of the Gawain-Poet.
[25] I think this might be best described as the western slopes of the Pennines, ranging perhaps from Stoke-on-Trent to Lancaster. The Gawain-Poet was very familiar with the Pennine moorland, and the Nero A.x manuscript has been localised near Holmes Chapel, just below the Pennine edge. Critics have often employed the location “Cheshire”, but a man from Chester would not have had any close familiarity with the Pennine uplands. I use the generic term “north west”.
[26] By defining our Universe of Discourse in this way we have already applied the first two criteria of the template: we have chosen a group of people who all satisfy the date and dialect requirements. It is of course totally irrelevant that the Universe of Discourse was introduced into set theory by Charles Dodgson (Lewis Carroll) from Daresbury in the heart of Sir Gawain and the Green Knight country.
[27] Before elimination of duplicates we have a population of 51×(18,000+10,500)/2 = 726,750. For one person of each age we have a total number of duplicates of 30×21+15×30+15×30 = 1530. If we now assume that the populations of each age are equal, we have 1530/81 = 18.889 average duplicates per person, and a final population of 726750-(18.889×(18,000+10,500)/2)+14250 = 471,833.
[28] By educated we cannot imply a university education: there were not many with that in the area, certainly not the 943 we arrive at with an estimate of 1 in 50, although as Bennett [p.73] says,“Sir Hugh Calveley cannot have been the only local knight to put his nephews through university”. Perhaps we should take “educated” to imply that a man could read and write English, have a good knowledge of Latin and French, be reasonably familiar with the Arthurian cycle, with classical history and literature, be familiar with the alliterative tradition of poetry, and be aware of the local geography, at least to include north Wales. Even this level of education considerably exceeded that of a younger brother of the minor gentry: Orme [ORME84] describes the education of an aristocratic boy as the attainment of basic literacy (reading and writing) followed by some Latin, but from the age of twelve concentrating on the arts of war. This is certainly in accord with the importance of war in fourteenth century Lancashire and Cheshire where the wars in France were the major source of wealth. However, it is conceivable that a younger son of the local gentry, bookishly inclined, might absorb a wider education from contact with local ecclesiastics and clerks, particularly if he happened to live near an abbey. Nevertheless, an education of the level posited here must have been a very rare occurrence, and an estimate of 1 in 50 of men or women between 20 and 50 is far too optimistic: 1 in 500 might still be short of the mark. The picture emerges of a young man who had been happy to spend a great deal of his time with books and listening to poetry, hardly an eldest son who would have been concerned with the estates, or a younger son who was bent on improving himself by war. Proximity to a good library in the formative years of his youth is indicated, together with a social status that gave him access to the library: a family of local gentry residing close to an abbey would fit the bill, particularly if a family member were part of the abbey establishment.
[29] There is little evidence of this awareness in England in the fourteenth century, the pentangle, with its inner structure occurs only very rarely, and the symbol generally appears to have a magical significance, which was strongly opposed by the church [HARDMAN99].
[30] The eldest sons of the minor gentry would be at home, learning and helping to run the family's estates, the best a younger son could do was to accept service in the household of some noble, or train for the clergy, and often both. By far the majority of the population of course were not younger sons of local gentry, they were the peasant population supporting the local gentry, and would have little or no possibility of learning the detail of courtly life.
[31] The smaller the probability the smaller the size of the intersection set. In principle the probability is the ratio of the sizes of the intersection set and the Universe of Discourse.
[32] Such negative evidence is, of course, very difficult to obtain.
[34] A rather dubious statistical operation.
[35] we can express the likelihood of finding a member of the population conforming to a requirement either as a fraction (e.g. 1 in 20) or as a probability (0.05, the reciprocal of the fraction)